2.5. Virtual short (virtual ground)

Figure 2-16 Negative-feedback amplifier (inverting amplifier)
Figure 2-16 Negative-feedback amplifier (inverting amplifier)

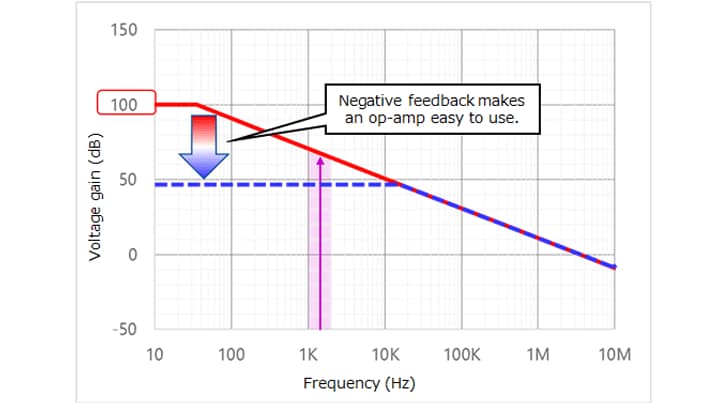
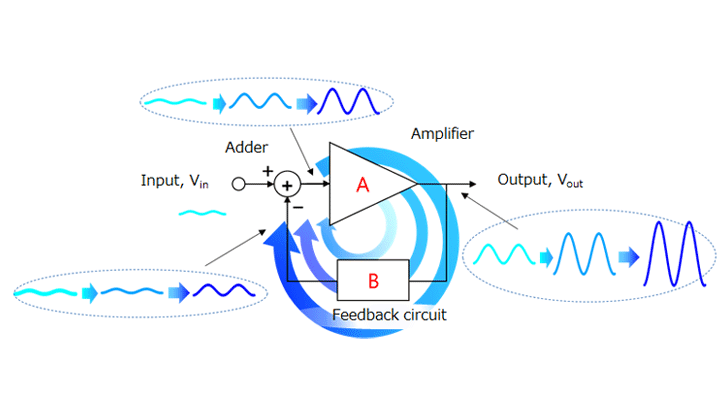
The closed-loop gain of an op-amp with negative feedback can be calculated easily using the concept of a virtual short-circuit (also known as a virtual short or virtual ground*).
The concept of a virtual short is that the VIN (+) and VIN (-) terminals of an op-amp with negative feedback have almost the same potential regardless of the input signal when it has a large open-loop gain.

Consider as follows to intuitively understand a virtual short.
An op-amp amplifies a difference in voltage between VIN(+) and VIN(-) by a factor of 100,000 or more (called the open-loop gain). However, a real op-amp has a finite output. Therefore, when a distortion-free output is obtained with an amplifier using an op-amp, the difference in voltage between the VIN(+) and VIN(-) inputs should be negligible.
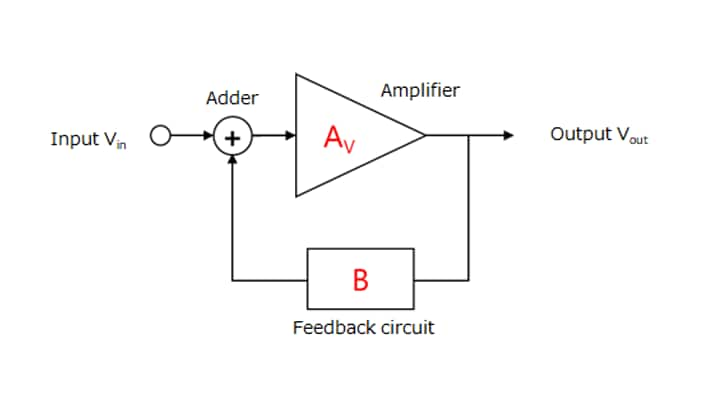
In the case of the negative-feedback amplifier (inverting amplifier) shown in Figure 2-16, the output is connected to the input in such a manner that an increase in output causes a decrease in input. As a result, the output signal fits between the power supply and ground. (Suppose, for example, that an inverting amplifier has an input voltage of 1 Vpp and a gain of 3 (R2 = 3 × R1). Then, the output voltage becomes 3 Vpp.)
At this time, the op-amp is operating with an open-loop gain of 100,000. Since the output voltage is 3 Vpp, the input voltage is 3 Vpp/100,000 = 30 μVpp. Hence, VIN(-) ≈ VIN(+).
Next, let’s use simple calculations to understand this. Figure 2-16 shows a negative-feedback amplifier (inverting amplifier) using an op-amp.

Equation 3 of the op-amp

Suppose that the op-amp is the ideal one. Then, the following are true:

  1. Infinite open-loop gain (AV)
  2. Infinite input impedance
  3. Zero output impedance

Since the input impedance is infinite, all of the current flowing through R1 (i1) flows through R2.

i1 ＝ (Vi – VIN(−)) / R1 = (VIN(−) - Vo) / R2          (1)

The output voltage of the op-amp is given by the equation: Vo = AV × (VIN(+) – VIN(−))  (2)
From Equations 1 and 2, VIN(+) is calculated as follows:

 

Because the output impedance is zero, we obtain VIN(＋) = VIN(−) from Equation 3.
Hence, the voltage at the VIN(−) input is equal to that of the V IN(＋) input connected to GND.
In this case, the condition of the VIN(−) input is called a virtual short.

* In a broad sense, a virtual ground is a node of a circuit that is maintained at a steady reference potential without being connected directly to a power supply or ground. In the circuit of Figure 2-16, VIN(-) is called a virtual ground since it is virtually equal to GND.

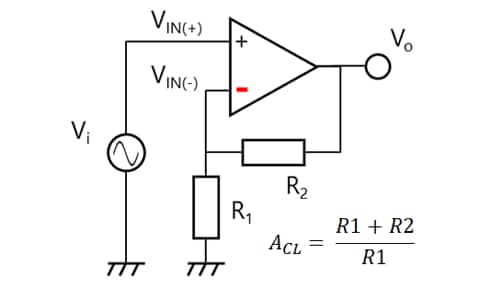
Next, let’s calculate the closed-loop gain (AV) of the noninverting amplifier shown in Figure 2-17 using a virtual short and the ideal op-amp. Let’s express the output voltage (Vo) as a function of Vi. From the concept of a virtual short, VIN(-) = VIN(+) = Vi.
Therefore, the current flowing through R1 (i1) is calculated as follows:

I1 = VIN(-) / R1 = Vi / R1

Figure 2-17 Noninverting amplifier
Figure 2-17 Noninverting amplifier

No current flows to the op-amp input since it has infinite impedance. Letting the current flowing through R2 be I2, I1 = I2. Hence, the voltage across R2 (VR2) is:

VR2 = R2 × I2 = R2 × Vi / R1

Hence, Vo is calculated as:

Vo ＝ VR1 + VR2
= Vi + R2 × Vi /R1 = Vi × (R1 + R2) / R1

AV = Vo / Vi = (R1 + R2) / R1

You can easily find the closed-loop gain equation.

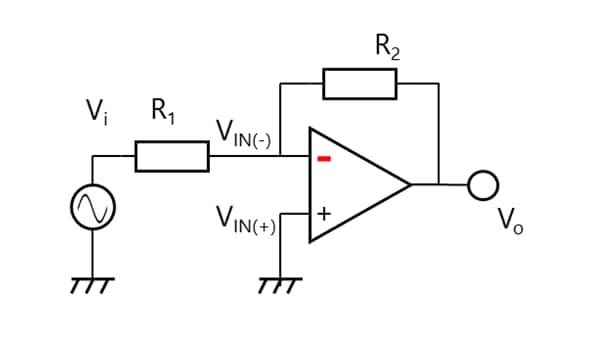
Figure 2-18 Inverting amplifier
Figure 2-18 Inverting amplifier

The closed-loop gain (AV) of the inverting amplifier shown in Figure 2-18 can also be calculated in the same manner.

VIN(-) = VIN(+) = 0 V (GND)
I1 = V1 / R1 = I2
Vo = VR2 = R2 × I2 = R2 × V1 / R1

Hence, the closed-loop gain is:

AV = Vo / Vi = R2 / R1

As described above, the closed-loop gain can be calculated easily using the concepts of a virtual short and the ideal op-amp.

Related information

■FAQ

Chapter2 Using an op-amp

2. Using an op-amp
세부 사항
2.1. Feedback (positive and negative feedback)
세부 사항
2.2. Open-loop and closed-loop gains (Increasing the bandwidth of an amplifier)
세부 사항
2.3. Oscillation
세부 사항
2.4. Basic op-amp applications
세부 사항

Related information

Back to Basics of Op-amps

A new window will open