-
My ToshibaSemicon
- 반도체 탑
-
애플리케이션Automotive
Body Electronics
xEV
In-Vehicle Infotainment
Advanced Driver-Assistance Systems (ADAS)
Chassis
IndustrialInfrastructure
BEMS/HEMS
Factory Automation
Commercial Equipment
Consumer/PersonalIoT Equipment
Healthcare
Wearable Device
Mobile
Computer Peripherals
-
제품자동차 디바이스
Discrete Semiconductor
다이오드
트랜지스터
로직 IC
Analog Devices
Digital Devices
Wireless Devices
※
: Products list (parametric search)
파워반도체※
: Products list (parametric search)
Isolators/Solid State RelaysPhotocouplers
Digital Isolators
Solid State Relays
Fiber Optic Transmitting Modules
※
: Products list (parametric search)
MOSFETsIGBTs/IEGTs바이폴라 트랜지스터※
: Products list (parametric search)
다이오드※
: Products list (parametric search)
마이크로컨트롤러모터 드라이버 ICIntelligent Power ICs※
: Products list (parametric search)
전원관리IC리니어 IC※
: Products list (parametric search)
범용로직IC리니어 이미지 센서기타 제품용 IC기타 제품용 IC
※
: Products list (parametric search)
-
개발/설계 지원
-
기술 자료
- 구매처
- 부품 번호 & 키워드 검색
- 상호 참조 검색
- 파라미터 검색
- 재고 확인 및 구매
This webpage doesn't work with Internet Explorer. Please use the latest version of Google Chrome, Microsoft Edge, Mozilla Firefox or Safari.
3글자 이상 입력하세요. Search for multiple part numbers fromhere.
The information presented in this cross reference is based on TOSHIBA's selection criteria and should be treated as a suggestion only. Please carefully review the latest versions of all relevant information on the TOSHIBA products, including without limitation data sheets and validate all operating parameters of the TOSHIBA products to ensure that the suggested TOSHIBA products are truly compatible with your design and application.Please note that this cross reference is based on TOSHIBA's estimate of compatibility with other manufacturers' products, based on other manufacturers' published data, at the time the data was collected.TOSHIBA is not responsible for any incorrect or incomplete information. Information is subject to change at any time without notice.
3글자 이상 입력하세요.
2.2. Open-loop and closed-loop gains (Increasing the bandwidth of an amplifier)
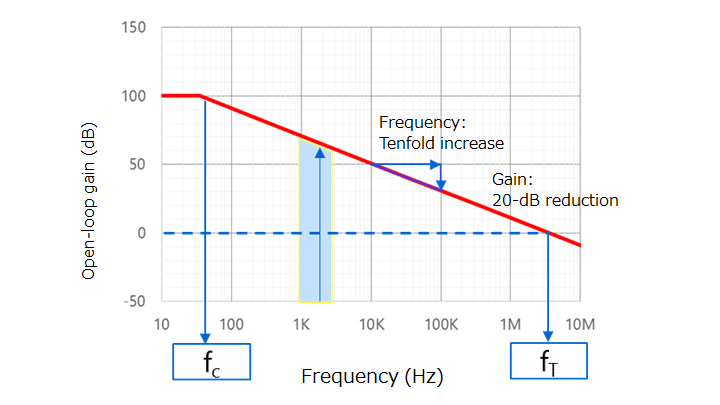
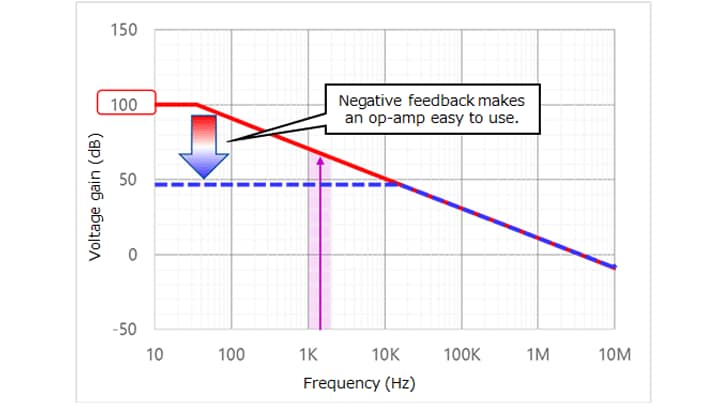
The open-loop gain (GV) of an op-amp has the same frequency characteristics as a first-order RC lowpass filter as shown in Figure 2-3. At frequencies higher than the corner frequency (fC) at which the open-loop gain is 3 dB lower than the DC gain, the open-loop gain decreases at a rate of 6 dB per octave (20 dB per decade). In this frequency range, the decibel open-loop gain of the op-amp (GV) decreases by 6 dB (i.e., the linear open-loop gain (AV) halves) when the frequency doubles. Hence:
fc × AV = constant
The frequency at which the gain is equal to 1 (0 dB) is called the unity gain cross frequency (fT). Therefore, the above equation can be restated as follows. This is called the gain-bandwidth product (designated as GBWP, GBW, GBP, or GB).
fc × AV = fT
Note that this equation is true in the frequency range in which the open-loop gain decreases at a rate of 6 dB per octave.
Now, let’s consider what occurs when an input signal with a frequency of 2±1 kHz is applied to an op-amp that has frequency characteristics as shown in Figure 2-3. In the case of an op-amp under this condition, the gain at 3 kHz is roughly 10 dB lower than the gain at 1 kHz. Normally, the op-amp cannot be used under this condition. Negative feedback solves this issue.
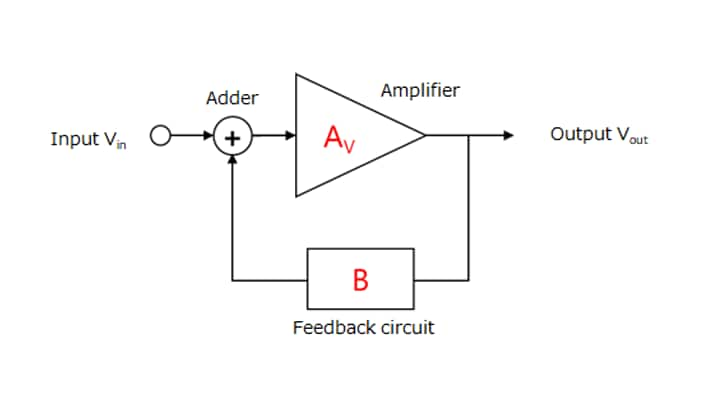
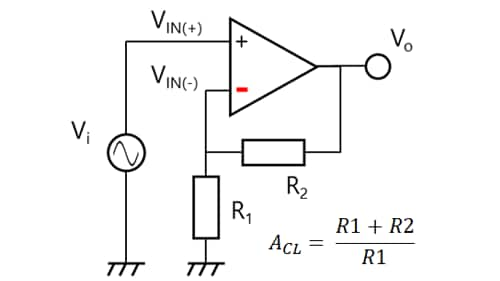
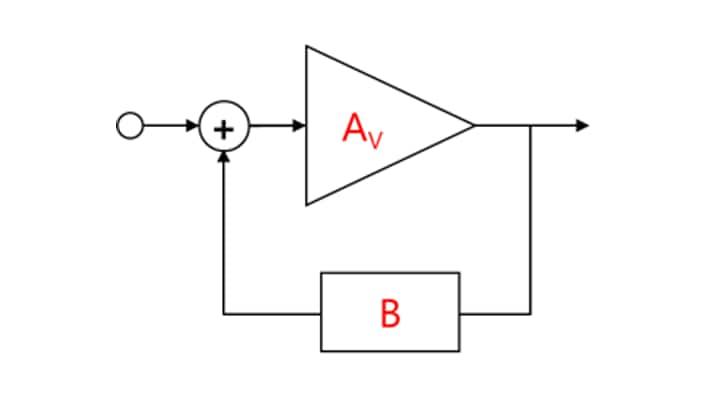
The input (Vin) and the output (Vout) have the following relationship. This relationship is called a closed-loop gain (represented as GCL in dB scale and ACL in linear scale). The 20 log rule is used to convert a linear voltage gain into a decibel voltage gain: G = 20 × log A.
Vout / Vin = ACL = AV / (1 + AV × B)
= 1 / {B (1 + 1 / AV × B)}
where AV is the open-loop gain of an amplifier and B is the feedback factor. (AV × B) is called the loop gain. The denominator, (1 + AV × B), is called the amount of feedback. In the case of negative feedback, AV × B < 0. An op-amp has a very high AV. Hence, | AV x B | >> 1. Therefore, the amount of feedback is calculated as (1 + AV × B) ≈ AV × B (loop gain). Hence, the above equation can be simplified as follows:
Vout / Vin = ACL = 1/B
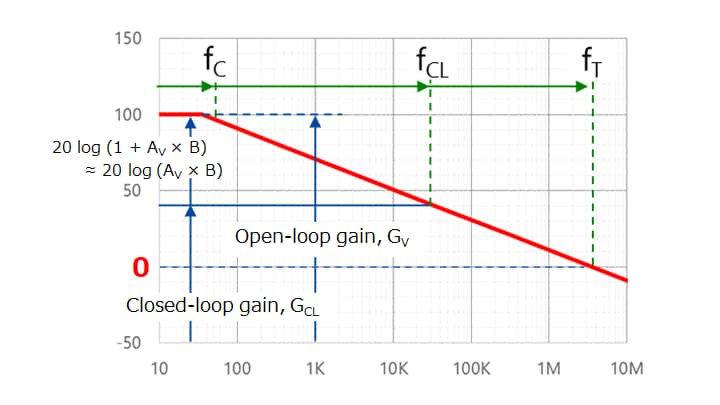
Figure 2-5 shows this relationship. The op-amp has a bandwidth of fC. With negative feedback, its closed-loop bandwidth expands to fCL. fCL is calculated as follows from the gain-bandwidth product equation:
fCL = fT / ACL
When the closed-loop gain (GCL) or the bandwidth (fCL) is insufficient, it is necessary to select an op-amp with high fT.
Related information
Chapter2 Using an op-amp
Related information
- Products
- Application Notes
- FAQs
- Parametric Search
- Stock Check & Purchase