2.2. Open-loop and closed-loop gains (Increasing the bandwidth of an amplifier)

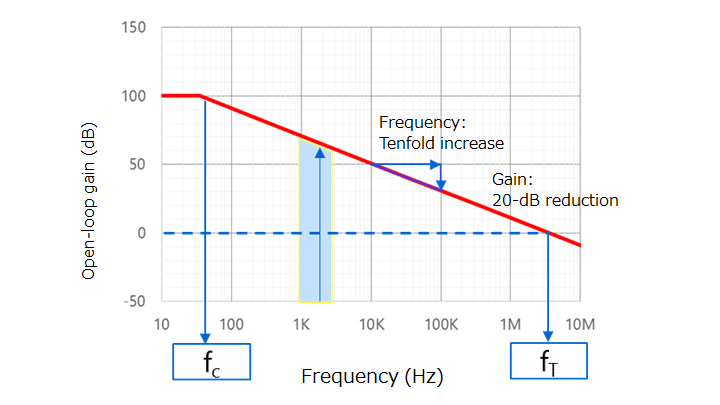
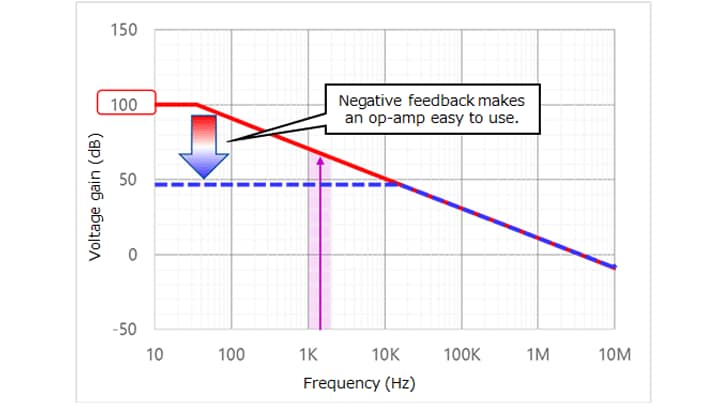
The open-loop gain (G_V) of an op-amp has the same frequency characteristics as a first-order RC lowpass filter as shown in Figure 2-3. At frequencies higher than the corner frequency (f_C) at which the open-loop gain is 3 dB lower than the DC gain, the open-loop gain decreases at a rate of 6 dB per octave (20 dB per decade). In this frequency range, the decibel open-loop gain of the op-amp (G_V) decreases by 6 dB (i.e., the linear open-loop gain (A_V) halves) when the frequency doubles. Hence:

f_c × A_V = constant

The frequency at which the gain is equal to 1 (0 dB) is called the unity gain cross frequency (f_T). Therefore, the above equation can be restated as follows. This is called the gain-bandwidth product (designated as GBWP, GBW, GBP, or GB).

f_c × A_V = f_T

Note that this equation is true in the frequency range in which the open-loop gain decreases at a rate of 6 dB per octave.

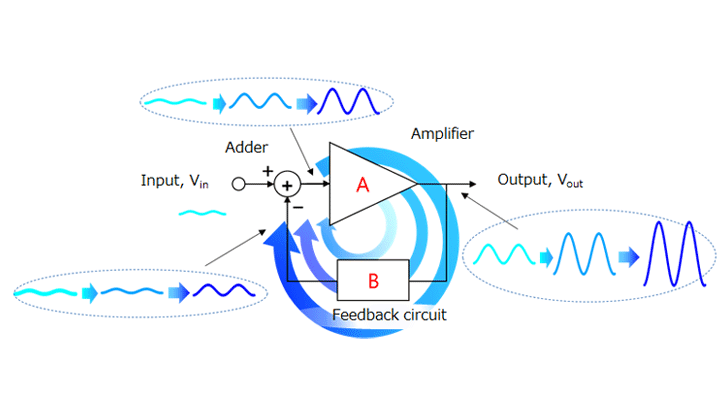
Now, let’s consider what occurs when an input signal with a frequency of 2±1 kHz is applied to an op-amp that has frequency characteristics as shown in Figure 2-3. In the case of an op-amp under this condition, the gain at 3 kHz is roughly 10 dB lower than the gain at 1 kHz. Normally, the op-amp cannot be used under this condition. Negative feedback solves this issue.

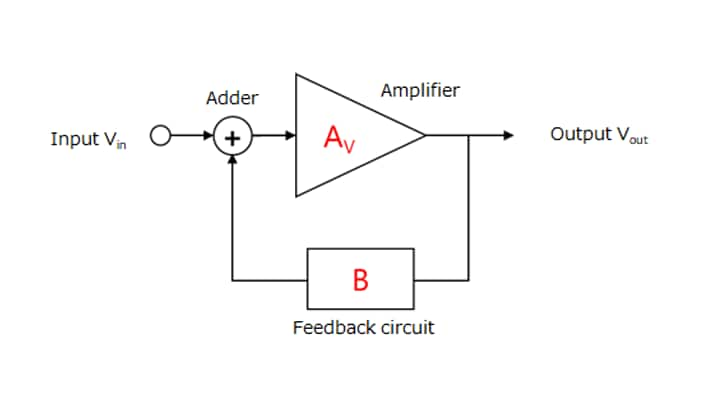
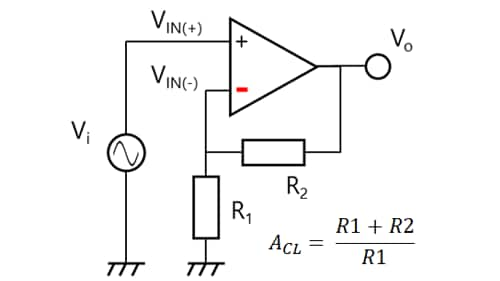
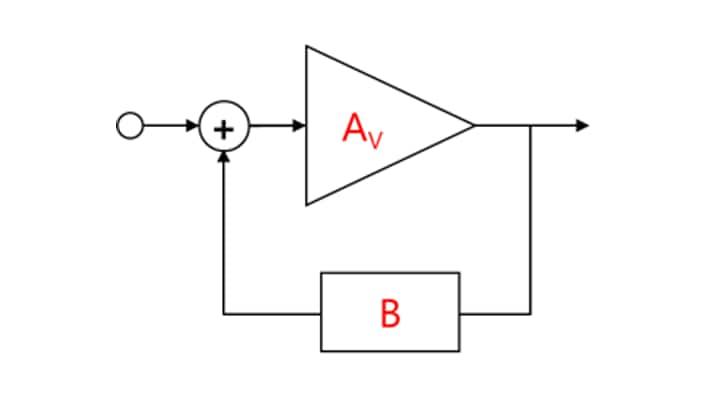
The input (V_in) and the output (V_out) have the following relationship. This relationship is called a closed-loop gain (represented as G_CL in dB scale and A_CL in linear scale). The 20 log rule is used to convert a linear voltage gain into a decibel voltage gain: G = 20 × log A.

V_out / V_in = A_CL = A_V / (1 + A_V × B)
　　　　　　     = 1 / {B (1 + 1 / A_V × B)}

where A_V is the open-loop gain of an amplifier and B is the feedback factor. (A_V × B) is called the loop gain. The denominator, (1 + A_V × B), is called the amount of feedback. In the case of negative feedback, A_V × B < 0. An op-amp has a very high A_V. Hence, | A_V x B | >> 1. Therefore, the amount of feedback is calculated as (1 + A_V × B) ≈ A_V × B (loop gain). Hence, the above equation can be simplified as follows:

V_out / V_in = A_CL = 1/B

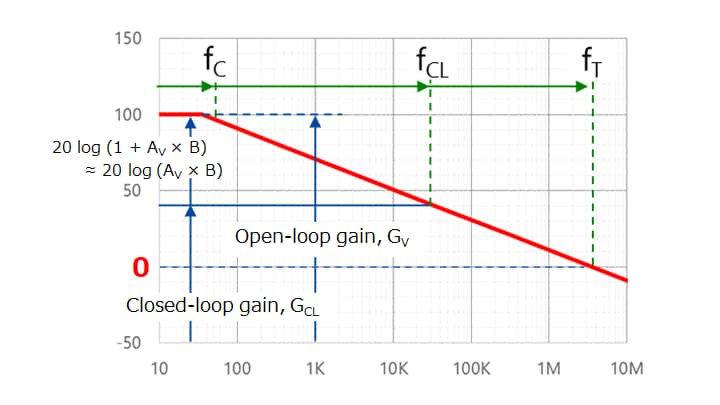
Figure 2-5 shows this relationship. The op-amp has a bandwidth of f_C. With negative feedback, its closed-loop bandwidth expands to f_CL. f_CL is calculated as follows from the gain-bandwidth product equation:

f_CL = f_T / A_CL