- General Top
- SEMICONDUCTOR
- STORAGE
- COMPANY
-
My ToshibaSemicon
- Semiconductor Top
-
ApplicationsAutomotive
Body Electronics
xEV
In-Vehicle Infotainment
Advanced Driver-Assistance Systems (ADAS)
Chassis
IndustrialInfrastructure
BEMS/HEMS
Factory Automation
Commercial Equipment
Consumer/PersonalIoT Equipment
Healthcare
Wearable Device
Mobile
Computer Peripherals
-
ProductsAutomotive Devices
Discrete Semiconductor
Diodes
Transistors
Logic ICs
Analog Devices
Digital Devices
Wireless Devices
※
: Products list (parametric search)
Power SemiconductorsSiC Power Devices
※
: Products list (parametric search)
Isolators/Solid State RelaysPhotocouplers
Digital Isolators
Solid State Relays
Fiber Optic Transmitting Modules
※
: Products list (parametric search)
MOSFETsIGBTs/IEGTsBipolar Transistors※
: Products list (parametric search)
Diodes※
: Products list (parametric search)
MicrocontrollersMotor Driver ICsIntelligent Power ICs※
: Products list (parametric search)
Power Management ICsLinear ICs※
: Products list (parametric search)
General Purpose Logic ICsLinear Image SensorsOther Product ICsOther Product ICs
※
: Products list (parametric search)
-
Design & Development
-
Knowledge
- Where To Buy
- Part Number & Keyword Search
- Cross Reference Search
- Parametric Search
- Stock Check & Purchase
This webpage doesn't work with Internet Explorer. Please use the latest version of Google Chrome, Microsoft Edge, Mozilla Firefox or Safari.
require 3 characters or more. Search for multiple part numbers fromhere.
The information presented in this cross reference is based on TOSHIBA's selection criteria and should be treated as a suggestion only. Please carefully review the latest versions of all relevant information on the TOSHIBA products, including without limitation data sheets and validate all operating parameters of the TOSHIBA products to ensure that the suggested TOSHIBA products are truly compatible with your design and application.Please note that this cross reference is based on TOSHIBA's estimate of compatibility with other manufacturers' products, based on other manufacturers' published data, at the time the data was collected.TOSHIBA is not responsible for any incorrect or incomplete information. Information is subject to change at any time without notice.
require 3 characters or more.
What is the maximum frequency at which an op-amp can be used?
To use an op-amp at high frequency, it is necessary to take two factors into consideration: slew rate and Unity Gain Cross Frequency (fT).
If the slew rate is low for the frequency used, the square wave will become a trapezoidal wave and the sine wave will become a triangular wave.
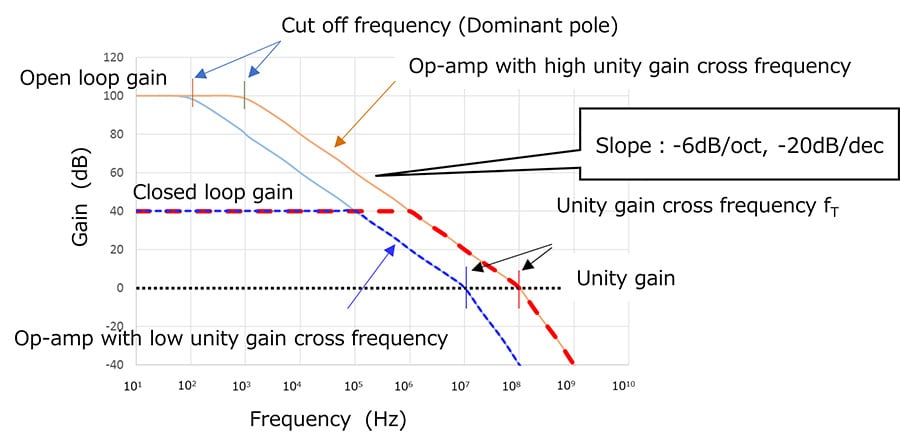
Voltage gain decreases at frequencies above the 3dB cutoff frequency of the open-loop gain. In this part, not only does the voltage gain factor vary from product to product, but if a signal with a wide bandwidth is input, the gradient of the amplification factor causes waveform distortion. Please apply negative feedback to the operational amplifier so that the gain is flat up to the operating band.
Also, be careful of oscillations at frequencies close to unity gain. There is an explanation in the op amp e-learning 2.3. Oscillation. Oscillation. please refer.
the op amp e-learning 2.3. Oscillation
- Slew rate (SR):
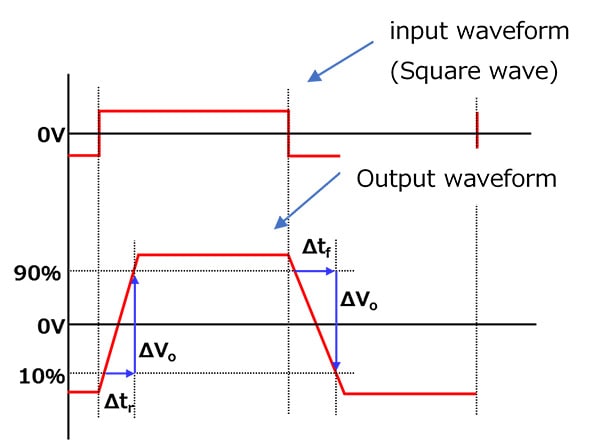
Even when the ideal rectangular waveform (a fast-rising signal) is applied to the input of an op-amp, its output does not provide the ideal rectangular waveform as shown in Fig. 3.
A change in output voltage per 1 μs is called a slew rate.
As shown in Fig. 3, in the case of an op-amp with a low slew rate, a rectangular input signal appears as a trapezoidal signal at the output, and a sinusoidal input appears as a triangular signal at the output.
- Unity Gain Cross Frequency (fT):
Frequency at which the open-loop gain becomes unity gain (0 dB)
As shown in Fig. 2, an op-amp with a higher cut-off frequency provides a greater bandwidth with the same closed-loop gain.
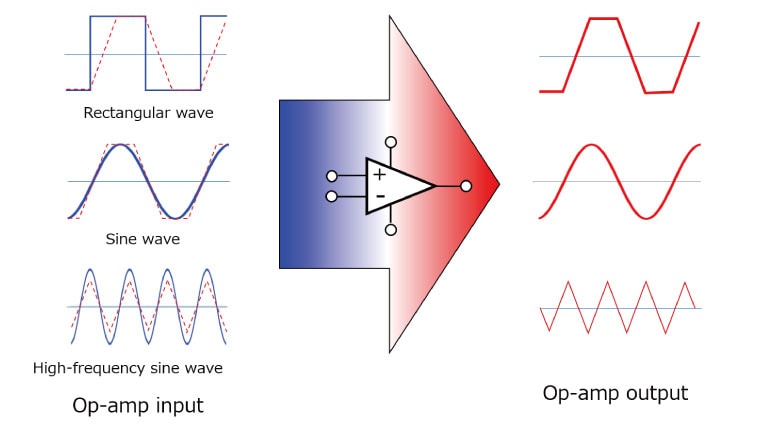
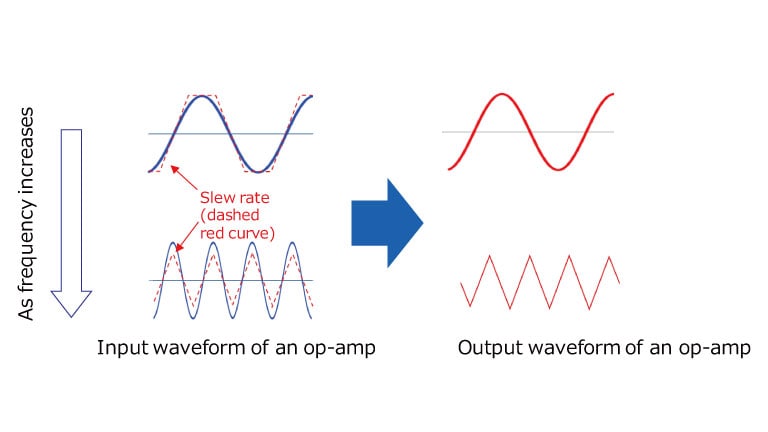
If you use an op amp with a low slew rate, the shape of the waveform will change and distortion will worsen.
Its maximum output frequency (fmax) can be calculated from the slew rate.For simplicity, we will first explain the case of using op-amp in unity gain.
The slew rate (SR) is expressed as:
SR = ΔVo / Δtr or ΔVo/ Δtf
Waveform distortion occurs when the maximum value of the output signal differentiated by time becomes higher than this SR.
Let the voltage of the input sine wave with an amplitude of A be Vin = Asinωt. Then, no waveform distortion occurs if the maximum change (differential value) in the amplitude of the input signal is less than the slew rate.
Since the differential value of the input signal is dVin / dt = Aωcosωt, its maximum value is Aω. Therefore, the maximum frequency that does not cause slew-inducted waveform distortion is theoretically calculated as follows, where A is the input amplitude.
SR = Aω =2πfmaxA
fmax = SR / 2πA
If there is no unity gain, the voltage gain of the amplification circuit is multiplied by Av, then Vo = Av x Vin.
The same can be said for unity gain.
dVout / dt = AvAω cosωt
SR = AvAω =AvA2πfmax
fmax = SR / 2πAAv
In practice, it is necessary to set fmax, allowing an adequate margin for the required frequency.
Related Links
The following documents also contain related information:



