ベクトルエンジンとベクトル制御
低消費、高効率でモーターを回すために、欠かすことのできないベクトル制御技術。
そのベクトル制御において、ソフトウェアの負荷軽減を実現できるベクトルエンジン(VE)の解説を、ベクトル制御技術と合わせて行っています。
近年、エアコンなどのモーター制御にベクトル制御という方法が使われるようになりました。モーターの回転を低速から高速まで効率よく制御できる高度な技術です。特に低速でのスムーズなモーター制御はベクトル制御無しでは実現できないと言ってもいいほどです。
ベクトル制御は非常に複雑な工程を使った制御方法で、それを理解するためには数学的な知識を必要とします。しかしながら、数式をなるべく使わずにベクトル制御のエッセンスを理解いただけるように解説します。
3相モーターを例にベクトル制御を紹介します。
まずは、3相モーターとそのドライバーの解説です。
3相モーターとドライバー
3相の交流波形は互いに120°だけ位相がずれた3つの正弦波からなります。この3つの交流をそれぞれ3つの端子に供給してローターを回転させるのが3相モーターです。モーターの回転数は交流の周波数で制御できます。つまり、ゆっくり回転させるには交流の周波数を小さくし、高速で回転させるためには周波数を大きくします。
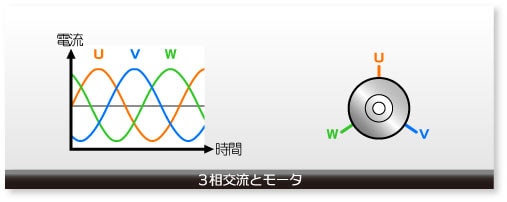
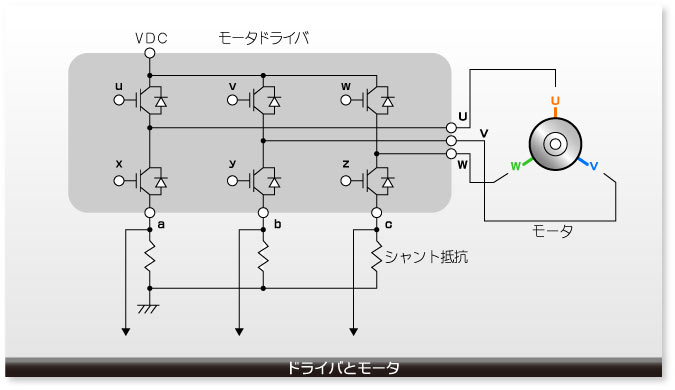
この3相モーターに3相の電圧(または電流)を直接与えるためにモータードライバーというICが使われます。ベクトル制御の場合、モータードライバーの基本回路は6個のトランジスター(トランジスターとそれに並列に接続されたダイオード)からなります。その6個のトランジスターのオンとオフの制御にそれぞれ6本の入力信号 u、v、w、x、y、およびz があり、また、3相直流モーターを電流駆動するための3つの出力端子 U、V、およびW があります。
さらに、出力端子U、V、Wそれぞれの駆動電流をモニターするための端子 a、b、およびcの3本の出力端子があります。
ベクトル制御の全容
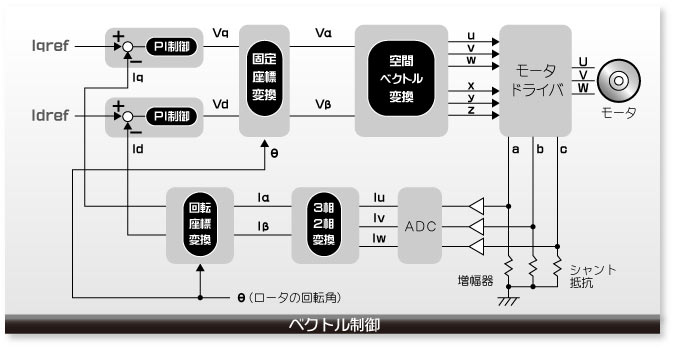
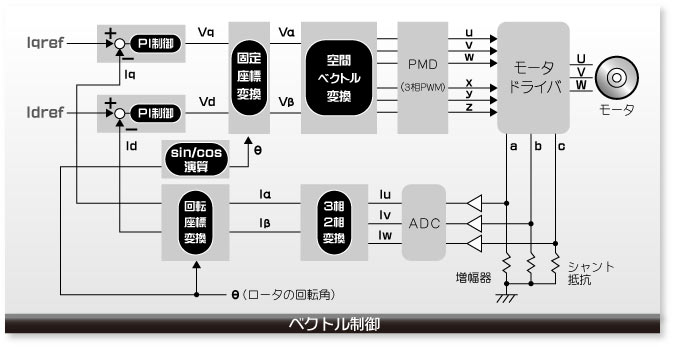
ベクトル制御の全体像を描いたものが下の図です。まず、ベクトル制御はモーターを駆動するU、V、およびWの波形をモニターすることから始まります。そのモニターのための信号がモーター・ドライバーの出力a、b、およびcです。このa、b、およびcの信号の振幅は非常に小さいのでアンプで増幅してADコンバーターに入力します。3相信号a、b、およびcはADコンバーターでデジタルの電流値Iu、Iv、およびIwに変換されたのち、さらに2相の電流値Iα、Iβに変換されます。
次に、この2相の電流は固定座標から回転座標へと座標変換され電流Id、Iqとなります。このId、Iqをあらかじめ決めておいた理想値 Iqref、Idrefと一致させるのがベクトル制御の目的です。Id、Iqはモーターの電流をモニターし、それを変換した値ですので理想値からは、ずれています。そこで、そのずれを無くすようにPI制御で補正します。その補正値は電流ではなく電圧の値Vd、Vqで与えられます。
次に、回転座標から固定座標に逆座標変換を行いVα、Vβが得られます。この2相の電圧Vα、Vβからモーター・ドライバーの3相入力信号u、v、およびwを導き出しますが、このときは単純な2相3相変換ではなく空間ベクトル変換という変換を行います。これにより、モーター・ドライバーの入力信号 u、v、w、および、それらの逆相の信号x、y、zが得られます。これにより、U、V、およびWの信号がモーターに与えられます。
以上でベクトル制御の1サイクルが終了しました。このサイクルを繰り返して、理想の回転状態を実現します。
それでは、この図に沿ってベクトル制御の各要素部分を、より詳しく説明します。
(1)駆動電流U、V、およびWのモニター、および、3相から2相への変換
3つの駆動電流U、V、Wはモニター端子a、b、およびcを介してモニターされます。ただし、これらのモニター信号の値は非常に小さいので、増幅器で信号増幅され、ADコンバーターに入力され、デジタル値に変換されます。変換されたデジタル電流値Iu、Iv、およびIwは、その後の計算に使われます。
さて、一般的に3つの信号を同時に扱うのは困難です。3つの信号が互いに何らかの関係をもって変化するため、3次元の空間での計算が必要となるからです。
そこで、計算をしやすいようにするため、3相を2相に変換します。変換にあたって、理想の3相交流では3つの正弦波を加えると0となるという性質を利用します。つまり、
Iu + Iv + Iw = 0
です。この条件をもとに3相を2相に変換しますが、2相に変換した後の2つの軸は互いに直交するものとします(90°で交わっているとします)。このような変換をClarke(クラーク)変換と呼びます。
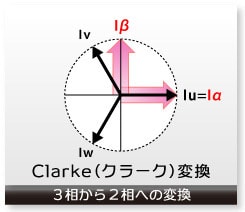
Clarke (クラーク)変換
3相の電流を(Iu、Iv、Iw)、2相変換後の電流を
(Iα、Iβ)とすると、
Iu + Iv + Iw = 0
Iα= Iu
Iβ= (Iu + 2Iv) / ![]()
となります。以上が、ベクトル制御における最初の変換である、3相から2相への変換です。
(2)回転座標変換
ベクトル制御での第二の変換は静止座標から回転座標への座標変換です。
実は、先ほど3相から2相に変換した電流値はローターを流れる電流値であり、ローターと一緒に回転しています。モーターを外から眺めているとローターがぐるぐる回っています。ところが、もし、ローターに乗ることができればローターは止まっていて、周りがぐるぐる回って見えます。つまり、ローターの回転と一緒に回転する座標では、ローターの上の2相電流は止まって見えます。静止して見える電流は直流として扱うことができます。
したがって、固定座標から回転座標へ座標変換すれば、計算が非常に簡単になります。固定座標から回転座標への変換をPark変換と呼んでいます。
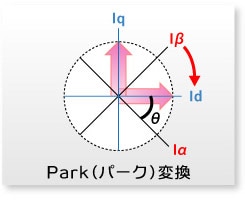
Park (パーク)変換
固定座標を(Iα、Iβ)、回転座標を(Id、Iq)、回転角をθとすると、
Id = Iα・cosθ+ Iβ・sinθ
Iq = -Iα・sinθ+ Iβ・cosθ
ところで、固定座標から回転座標へ変換するためにはローターの回転角θの値が必要です。つまり、ローターが今までにどれだけ回転したかがわからないと回転座標への変換ができません。実は、回転角の情報は何らかの別な手段で手に入れます。たとえば、回転用のセンサーであるインクリメンタル・エンコーダーなどでローターの回転角、および、回転速度を見出すことができます。
ここでは回転角はわかっているとして話を進めます。
(3)PI制御
ベクトル制御の半分の工程が終わりました。
ここまで来ますと、2相の電流Iq、Idの値がそれぞれの理想値より大きいか小さいかをチェックして、大きい場合は電流を減らす方向で、また、小さい場合は電流を増加する方向で制御することになります。
この部分ではPI制御を行うのが一般的です。PI制御はP制御(比例制御)とI制御(積分制御)を並列に行うもので、理想値と実測値との差に応じて増幅制御するのがP制御、その差の積分値に応じて増幅制御するのがI制御です。(IqとId の理想設定値はIqref、Idref としています。)
PI制御の入力は2相の電流値ですが、出力は2相の電圧値です。電流値ではなく電圧値とするのは、ベクトル制御の最終出力であるモータードライバーの入力信号が電流値ではなく電圧値だからです。
次に、PI制御を通して得られた2相の電圧値Vg、Vdを回転座標から固定座標に戻します。
そのためには、今、回転座標系で計算した電圧値を回転座標から降りて、固定の座標系で計算しなおさなければなりません。以前、固定座標系から回転座標系へ変換しましたが、その方法の逆変換を行います。この変換を逆Park変換と呼びます。このとき必要となるのが回転角ですが、それは、固定座標から回転座標への変換時にすでにわかっていますので、それを使います。
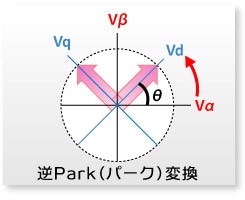
逆Park変換
Vα= Vd・cosθ-Vq・sinθ
Vβ= Vd・sinθ+Vq・cosθ
(4)空間ベクトル変換
いよいよベクトル制御も大詰めとなりました。最後の変換が空間ベクトル変換です。
ゴールは目前ですが、空間ベクトル変換とはどんな変換なのか、見てみましょう。ここが一番難しいと思います。
空間ベクトル変換で、2相電圧を3相電圧に逆変換をします。これにより、モータードライバーの3相の入力波形u、v、wおよび、その逆位相波形x、y、zが得られます。
モーターを制御する3相交流は互いに120°だけ位相がずれた正弦波でした。そこで、まず、120°だけずらした3つの軸を用意します。それぞれの軸は3次元のベクトル表記で、それぞれ、(100)、(010)、(001)となります。
次に、それぞれの軸を原点を中心に反対方向に延長します。すると、(100)の延長線は(010)と(001)の中間に来ます。そこで、この軸は (011)となります。同様に、(010)の延長線は(101)、(001)の延長線は(110)となります。これにより、6つの象限が作られます。ここでは各象限をセクターと呼びます。
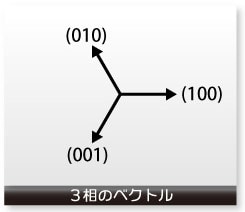

次に、2相の電圧Vα、Vβをこの空間に置き、ベクトル合成します。その合成電圧Vはローターと一緒に回転しますので、今作られた6つのセクターを順次、渡り歩くことになります。

ここで、空間を区切る6本の軸について説明します。
今、セクター0に電圧ベクトルVがある場合、このVを2つの軸 (100) と(110) のベクトルに分解します。(100)の成分を t1、(110)の成分をt2とすると左下の図が得られます。
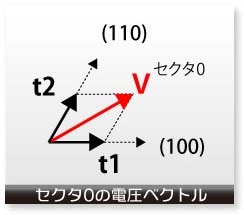
3相のベクトル(100)、(010)、(001)は、実は、モータードライバーの(u,v,w)に対応しています。(100)はu、(110)はuとvですので、
u=t1+t2
v=t2
となります。では、wはどうなるかと言いますと、セクター0の軸は (100) と (110) ですのでこれを見る限り常にw=0です。しかし最終的な波形を考慮して、次のようにwを決めます。
まず、6つのセクターの図で (000) と (111) の軸が無いことに注目します。(000) はu=v=w=0 ですのでドライバーのVDC側のトランジスターがすべてオフの状態で、ドライバーはモーターに電流を供給することができません。一方、(111) はu=v=w=1で、このとき反転入力x=y=z=0となります。つまり、今度はGND側の3つのトランジスターがすべてオフとなりますので、やはり、ドライバーは電流を供給できません。ですから、(000) と (111) は「モーターに向かって何もしない」動作となります。
さらに、空間ベクトル変換ではドライバーに入力する波形を作るために、ある一定の周期Tを決めてあります。電圧ベクトルVはローターと共に回転していますが、周期Tは非常に短い時間であり、この周期の間、電圧ベクトルVは静止しているとみなします。
今、セクター0にある電圧ベクトルVはt1とt2に分解されました。周期Tを、
T=t1+t2+t3
と定義しますと、t3の時間はセクター0では「何もしない時間」であり、このとき(uvw)は(000)もしくは(111)となります。
このようにして求められた u、v、およびwの波形が下図に示されています。波形の対称性を考慮してt1、t2は1/2に、t3は1/4を単位として波形が組み立てられていますが、1周期全体で見ますとu、v、およびwが1である時間は以下のようになります。
u=t1+t2+t3/2
v=t2+t3/2
w=t3/2
u、v、およびwのt3/2の項はu=v=w=1であり、何もしない時間です。一方、u=v=w=0の何もしない時間がやはり t3/2 だけあり、トータルでt3の何もしない時間が確保されていることがわかります。
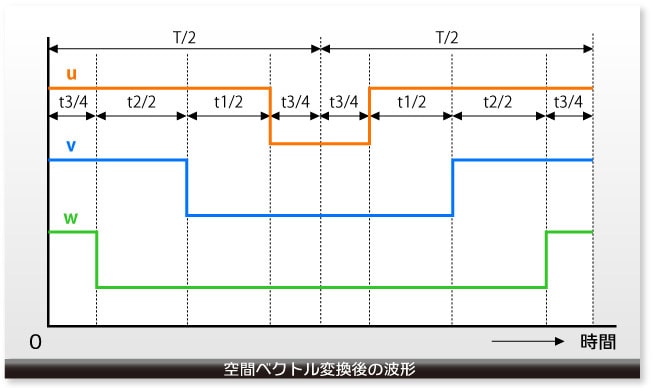
これで、ようやく、電圧ベクトルV(2相)を空間ベクトル変換で(u,v,w)の3相信号に変換できました。これで、一つの電圧ベクトルに対する空間ベクトル変換が完了しました。
では、電圧ベクトルVをさらに回転させてみましょう。電圧ベクトルVが各セクターを順次回転して通過した場合、u、v、wの t1、t2の値は下図のように変化します。なお、x、y、zはそれぞれu、v、wの反転波形として得られます。

ようやく、空間ベクトル変換によりu、v、w およびx、y、z の信号波形が得られました。
これで、ベクトル制御の全体が見えました。
ベクトル制御がいかに、複雑な工程を経てモーターを制御しているかをご理解いただけたと思います。
こんなに大変な制御ですが、モーター制御専用のマイクロコントローラーが出てきて
ベクトル制御が効率よくできるようになっています。
(5)正弦波
U、V、Wの実質的な電流はそれぞれu-v、v-w、w-uとなります。これらの電流をローターの回転角のグラフに描きますと、互いに120°だけ位相が異なる3相の正弦波形が得られます。
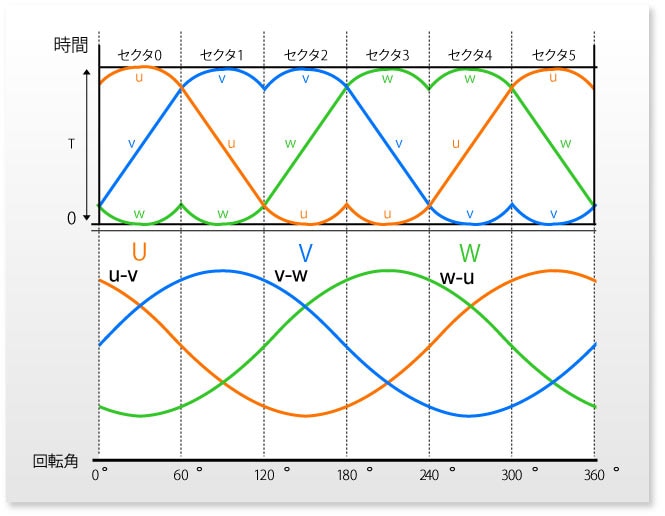
これにより、空間ベクトル変換がモータードライバーのトランジスターを駆動するu、v、wの信号を作り出す有効な方法であることを確認できました。空間ベクトル変換により3相モーターの入力信号U、V、Wをきれいな正弦波形として実現できるのです。
ベクトルエンジンは何をするの?
さて、ベクトル制御がどういうものが分かったところで、ベクトルエンジンは何をするものか説明をします。
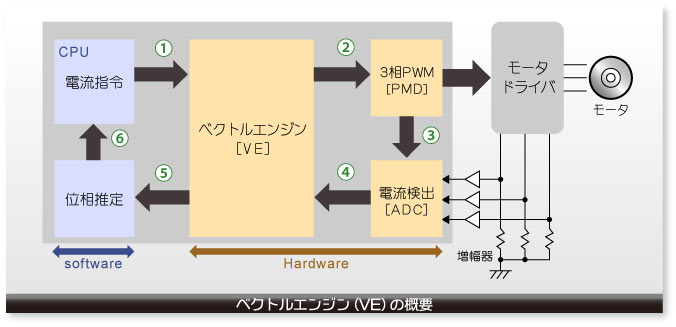
ベクトルエンジン自体は、ベクトル制御で必要な仕事の一部を、CPUに代わり、処理を行うハードウェアですが、このハードウェアを内蔵することにより、“ベクトル制御”という大枠で、大きな役割が実現できます。
それは、ベクトル制御で必要な周辺回路であるベクトルエンジン(VE)、モーター制御回路(PMD)及び、ADコンバーター(ADC)を、CPUを介さずに連動して動作させることです。
要するに、各周辺回路のデータの受け渡しを自動的に実行し、各周辺回路の起動タイミングを自動的に判断して処理を行います。
これによって、CPUは、ベクトル制御に対する処理が大幅に軽減できるという大きなメリットが生まれます。
ベクトル制御の全体図で、各仕事をどこが受け持つか見てみましょう。
①目標電流値 Iqref、Idref及び、ローターの回転角θをベクトルエンジンに設定します。
⇒ CPU
②相出力電圧値(U,V,Wの出力電圧に相当するパルス幅)を、PMDに設定します。
ADコンバーターの変換開始タイミングを計算し、そのタイミングをPMDにします。
⇒ VE
③PMD回路が、新たなU,V,Wに与える電圧(PWM)を出力し、ADコンバーターに変換開始信号を送信します。
⇒ PMD
④ADコンバーターは変換を終了すると、終了信号をベクトルエンジンに送信します。
⇒ ADC
⑤AD変換結果を取り込みフィードバック電流Id,Iqを算出し、CPUに割り込みを要求します。
⇒ VE
⑥割り込みを受けてソフトウェアでローターの角度算出、新たな電流指令値を算出します。
⇒ CPU
もうひとつは、ベクトルエンジンのハードウェア自身の仕事です。
ベクトル制御では、固定座標変換、空間ベクトル変換、3相2相変換、回転座標変換など、複雑な演算を行う必要があります。
それら複雑な演算をソフトウェアで、CPUで実行するには、複雑なプログラムを作る必要があります。
また、CPUの実行時間も長くかかり、色々な仕事があるCPUには、大きな負担になってしまいます。
では、実際にどの仕事をベクトルエンジンが行うのでしょうか。
- SinCosin演算
- 電流制御(PI制御)
- 固定座標変換
- 空間ベクトル変換
- 2相3相変換
- 回転座標変換
これら6つの仕事を実行するのがベクトルエンジンです。
このように、ベクトルエンジンは、ベクトル制御を行うのにたいへん便利なハードウェアなのです。
おわかりいただけましたでしょうか。かなり難しい内容ですが、さらにベクトル制御を詳しくお知りになりたい方は、専門書を参照していただきたいと思います。
また、東芝セミコンダクター&ストレージ社では、無料セミナーを開催していますので、ぜひご参加ください。
製品紹介
TX03シリーズ M370グループ TMPM375FSDMG
東芝独自のベクトルエンジンを内蔵することにより、モーターのベクトル制御に欠かせない基本的な処理(座標変換、相変換、SIN/COS演算)や、電流制御に使用されるPI制御の実行をハードウェアで行い、ソフトウェアの負荷を大幅に削減することが可能となりました。


