-
My ToshibaSemicon
- セミコンダクタートップ
-
アプリケーション車載
ボディエレクトロニクス
xEV
インフォテインメント
産業用機器業務用機器
民生/個人用機器 -
製品車載用デバイス
ディスクリート半導体
ダイオード
トランジスター
汎用ロジックIC
アナログデバイス
※
: 製品一覧(パラメトリックサーチ)
パワー半導体※
: 製品一覧(パラメトリックサーチ)
アイソレーター/ソリッドステートリレー(SSR)フォトカプラー
デジタルアイソレーター
ソリッドステートリレー (SSR)
光伝送モジュール
※
: 製品一覧(パラメトリックサーチ)
MOSFETIGBT/IEGTバイポーラートランジスター※
: 製品一覧(パラメトリックサーチ)
ダイオード※
: 製品一覧(パラメトリックサーチ)
マイクロコントローラーモータードライバーインテリジェントパワーIC※
: 製品一覧(パラメトリックサーチ)
パワーマネージメントICリニアーIC※
: 製品一覧(パラメトリックサーチ)
汎用ロジックICリニアーイメージセンサーその他専用ICその他専用IC
※
: 製品一覧(パラメトリックサーチ)
-
開発/設計支援
-
知る/学ぶ
- ご購入
- 品番・キーワード検索
- クロスリファレンス検索
- パラメトリック検索
- オンラインディストリビューター在庫検索
本機能は Internet Explorer 11 ではご利用頂けません。最新のGoogle Chrome, Microsoft Edge, Mozilla Firefox, Safariにてご利用ください。
品番は3文字以上指定して下さい。 複数品番の検索はこちら。
クロスリファレンスでは参考品名が表示されますので、製品に関する最新の情報をデータシート等でご確認の上、単独およびシステム全体で十分に評価し、お客様の責任において適用可否を判断してください。参考にしている情報は、取得した時点の各メーカーの公式情報に基づいた当社の推定によるものです。当社は、情報の正確性、完全性に関して一切の保証をいたしません。また、情報は予告なく変更されることがあります。
品番は3文字以上指定して下さい。
オンラインディストリビューターが保有する東芝製品の在庫照会および購入が行えるサービスです。
インバーター制御
マイクロコントローラーを使って「インバーター制御」を行うことは、今や、当然の技術のように考えられています。市場からの強い要望に答えるべく、当社は、インバーター制御に特化したマイクロコントローラー製品を開発・製造・販売しており、さらに、製品群の拡充を推進しております。
インバーター制御
インバーター制御とは
インバーター制御とはどのような技術なのでしょうか。簡単にご紹介したいと思います。
インバーター制御とは、一般的には「直流を交流に変換すること」を意味します。よく知られていますように、直流とは、例えば乾電池が出力する電圧のように、時間にかかわらず一定のまま変化しない電圧のことです。これに対して、交流は時間とともに変動する電圧のことで、一般の商用電源のように 50Hz、または、60Hz の周期的な振動をする電圧を例としてあげることができます(ここで「電圧」と書きましたが、これは「電流」と置き換えることができます)。
インバーター制御は、エアコンや洗濯機のモーターの制御(電力を動力に変換)をしたり、IH 調理器のヒーター用熱源として使われたり、太陽電池で発電された電力を商用の電力に変換するパワーコンディショナーに使われるなど、広範囲に使用されています。

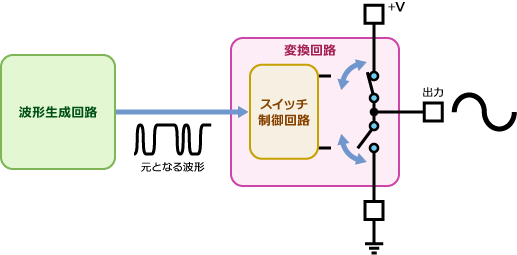
インバーター制御を行う回路は、大きく分けて2つの機能回路から成り立っています。インバーター出力の交流波形の「元となる波形」を作る「波形生成回路」と、その「元となる波形」を受け取り、交流に変換して出力する「変換回路」です。
では、どうやって直流を交流に変換するのでしょうか。まず、「波形生成回路」はある計算に基づいて、長さが異なるパルスの列を作製します。これが「元となる波形」です。どういう計算を行うのかは後ほど解説します。「波形生成回路」からパルス列を受け取る「変換回路」は、交流電圧を出力するための複数のスイッチを持っています。一つのスイッチには直流電圧が、また別のスイッチには基準電圧(GND)が供給されています。このスイッチは、「元となる波形」に合わせてオン、またはオフを繰り返し、出力端子から交流電圧を出力します。図に変換回路の概略を示しました。ここでは簡単化のためにスイッチは2個しか描かれていませんが、実際の回路ではもっと多くのスイッチが複雑に動作し、交流出力を作り出しています。
今回はマイクロコントローラーの役割を説明するのが目的ですので、「変換回路」についてはこれ以上の解説は割愛させていただきます。
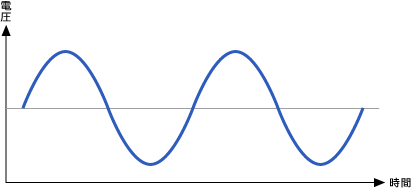
サイン・カーブ(正弦波形)
インバーター制御で交流を作る場合、その波形をサイン・カーブ(正弦波形)にしたい場合が数多くあります。例えば、モーター駆動の場合、サイン・カーブがモーターを最も滑らかに駆動し、しかも、消費電力が最少で済む可能性が高いからです。また、パワーコンディショナーでは、商用電力(100V 50Hz/60Hz)を生成しなければなりませんが、その電圧波形はサイン・カーブそのものです。従って、ここからは「波形生成回路」がどうやってサイン・カーブ(正弦波形)を作り出すかを説明します。
まず、理想的なサイン・カーブを想定します。インバーター制御で、このサイン・カーブを作ることを目標としましょう。
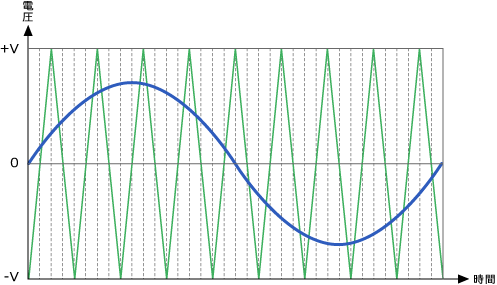
このサイン・カーブを作るための「元となる波形」を作る手順を紹介します。前述したように「変換回路」がサイン・カーブを出力しますが、その「変換回路」が出力できる最大の電圧を +V、最小の電圧を-Vとします。また、理想とするサイン・カーブの振幅はそれよりも小さいとします。
最初に行うことは、サイン・カーブを時間軸(横軸)方向に細分化し、それぞれの分割された区画に合わせて、適当な大きさの二等辺三角形を描くことです。
次に、サイン・カーブと二等辺三角形の連続波形とを比較して、サイン・カーブの電圧が大きいときを「1」、小さいときを「0」としてグラフを描きます。すると、幅の異なる四角形のパルス列を得ることが出来ます。実は、これが先ほどから何度も出てくる「元となる波形」なのです。
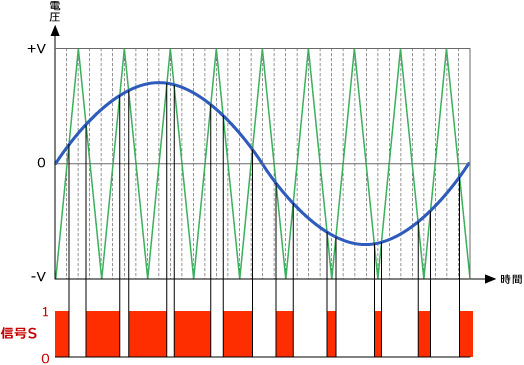
「元となる信号S」を見るとサイン・カーブの高いところがより広く、低いところがより狭いパルスとなっています。もう少し分かりやすくするために、信号Sの隙間を、各四辺形の面積を変えないようにして埋めてみました。(ただし、これは理解を容易にするためだけの概念波形です。実際にはこの波形「信号Sa」は存在していません。)こうすると、この信号Saがサイン・カーブを代表していることが分かります。容易に想像できますが、横軸の分割をより細かくして、二等辺三角形の数を増やして行きますとこの「元となる信号」の四辺形は数が増えて、より細くなり、その結果、信号Saはますますサイン・カーブに近づいていきます。
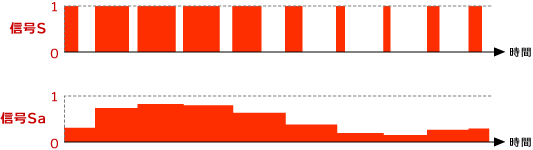
ところで、「元となる信号」のような、高さは一定で、幅の異なるパルス列を用いて任意の波形を作る方法を PWM (Pulse Width Modulation) と呼びます。このように、インバーター制御はPWMを使って実現されるのです。
フィードバック制御
「変換回路」が出力するサイン・カーブを受け取るものは、例えば、モーターやヒーターなどですが、電気的には「負荷」と呼ばれます。この負荷がサイン・カーブからエネルギーをもらうわけで、負荷のエネルギー消費量が大きいと、本来のサイン・カーブが捻じ曲げられ、波形が変化してしまいます。例えば、負荷が付いたために「変換回路」の出力波形の振幅が理想波形よりも小さくなったりします。
従って、このままでは理想のサイン・カーブは得られません。そこで、次のような新たな仕組みを取り入れます。まず、「変換回路」の出力端子に、どのような波形が出力されているかをチェックするモニター機能を追加します。そのモニター出力信号と理想のサイン・カーブとの大小を計算し、その結果に応じてPWM のパルス幅を調整します。つまり、理想波形の PWM 出力と検出された実際の波形を比較して、振幅が小さい場合は PWM のパルス幅を伸ばすということをします。これを何回か繰り返すと今度は「変換回路」の出力の振幅が理想波形より大きくなることもあります。その場合は、PWM のパルス幅を狭め、変換回路の出力振幅を下げ、理想波形に近づけます。
このように実際の出力波形をチェックして、理想状態との差を検出し、その差の情報を生成回路に与えることにより、最終出力を理想状態に近づける方法を、一般的にフィードバック制御と呼んでいます。この制御により、負荷が付いたときでも理想のサイン・カーブが得られるようになります。
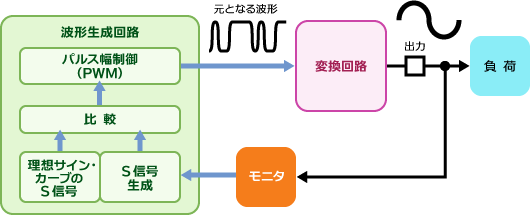
インバーター制御に必要な回路
ここまでで、インバーター制御の概念は理解していただいたと思います。では、実際にどのような回路を用いてそれを実現するのでしょうか。必要な回路は、「変換回路」の出力をモニターする回路、二等辺三角形を作る回路、二等辺三角形とモニター信号の大小を検出する回路(S信号の生成回路)、モニター信号のS信号と理想サイン・カーブのS信号との比較回路、理想サイン・カーブのS信号を保存しておく回路、PWMパルスを出力する回路、それに、もちろん、「変換回路」です。
一つ一つ見てみましょう。
(1) 「変換回路」の出力をモニターするためにはADコンバーターを使います。「変換回路」の出力はアナログ値ですので、これをデジタル値に置き換えて二等辺三角形のカウント値(これはデジタル)との大小の比較を行います。
(2) 二等辺三角形の波形を作るにはカウンター回路が使われます。少し早い周波数のクロックで、規則正しくインクリメントし、ある特定の値になったらデクリメントするというカウンターがあれば、そのカウント値が二等辺三角形を作ってくれます。
(3) 大小比較はデジタル計算回路が行います。
(4) 理想のサイン・カーブを作るためのS信号はメモリーに保存しておきます。
(5) PWM パルスを作るためには専用のパルス幅制御回路を用意します。
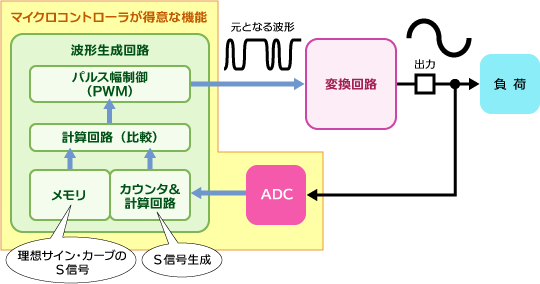
このように、インバーター制御に必要な回路を見てみますと、ほとんどは通常のマイクロコントローラーに存在している回路であり、特に、PWM機能を搭載するマイクロコントローラーがインバーター制御に最適であることが理解いただけると思います。
以上で、インバーター制御の説明を終えますが、ここでの説明は非常に単純化した例をもとに、インバーター制御とは何かを解説したもので、実際の方式、回路はもっと複雑なものです。
より詳しい説明は、すでに出版されているパワーエレクトロニクスの専門書に譲りたいと思います。


